浮点数累加的精度损失如何避免？

上一讲我们讲到，浮点数0.3在计算机中的表示不是准确的。

但是如果我们有个需求是累加1000万个0.3，该怎么办？

package main

import "fmt"

func main() {
	var sum float64
	var x float64 = 0.3
	for i := 0; i < 10000000; i++ {
		sum += x
	}
	fmt.Println(sum)
}

得到的结果显而易见是不正确的。

得到结果为$2.9999999996692175 \times10^6$，但是我们期望的结果是$3\times10^6$。

一个常见的应用场景是，在一些“积少成多”的计算过程中，比如在机器学习中，我们经常要计算海量样本计算出来的梯度或者 loss，于是会出现几亿个浮点数的相加。每个浮点数可能都差不多大，但是随着累积值的越来越大，就会出现“大数吃小数”的情况。这么大的误差显而易见是无法接受的。

当然，肯定有人已经解决了这个问题，并且已经封装好了库给你使用。但是你真的不想弄清楚这是如何避免精度的损失么？

golang decimal库

首先我们用一些别人封装好的库来实现避免精度的损失。

package main

import (
	"fmt"

	"github.com/shopspring/decimal"
)

func main() {
	var x float64 = 0.3
	sum := decimal.NewFromFloat(0.0)
	for i := 0; i < 10000000; i++ {
		newSum, _ := sum.Float64()
		sum = decimal.NewFromFloat(newSum).Add(decimal.NewFromFloat(x))
	}
	fmt.Println(sum)
}

结果完全正确，精度没有任何损失。

缺点就是很慢，因为库里面多了很多的转换等操作。

这是没有办法的事，所以在高性能的情况下，我们需要自己去实现优化，这就是学习数据结构与算法最大的用处了。

自己实现Kahan Summation

算法逻辑：

• 每次计算过程中，都用一次减法把当前加法计算中损失的精度记录下来
• 然后在后面的循环中，把这个精度损失放在要加的小数上
• 最后再做一次运算

package main

import "fmt"

func main() {
	var sum float64 = 0.0
	var c float64 = 0.0
    var x float64 = 0.3
	for i := 0; i < 10000000; i++ {
		y := x - c
		t := sum + y
		c = (t - sum) - y
		sum = t
	}
	fmt.Println(sum)
}

答案完全正确，是我们想要的结果。

我们将精度损失等变量的值打印出来。

package main

import (
	"fmt"
	"time"
)

func main() {
	var sum float64 = 0.0
	var c float64 = 0.0
	var x float64 = 0.3
	for i := 0; i < 10000000; i++ {
		y := x - c // 减法
		fmt.Printf("y: %.20f\n", y)
		t := sum + y // 相加有精度损失
		fmt.Printf("t: %.20f\n", t)
		c = (t - sum) - y //丢失的精度
		fmt.Printf("c: %.20f\n", c)
		sum = t
		fmt.Printf("sum: %.20f\n", sum)
		time.Sleep(time.Second)
	}
	fmt.Println(sum)
}

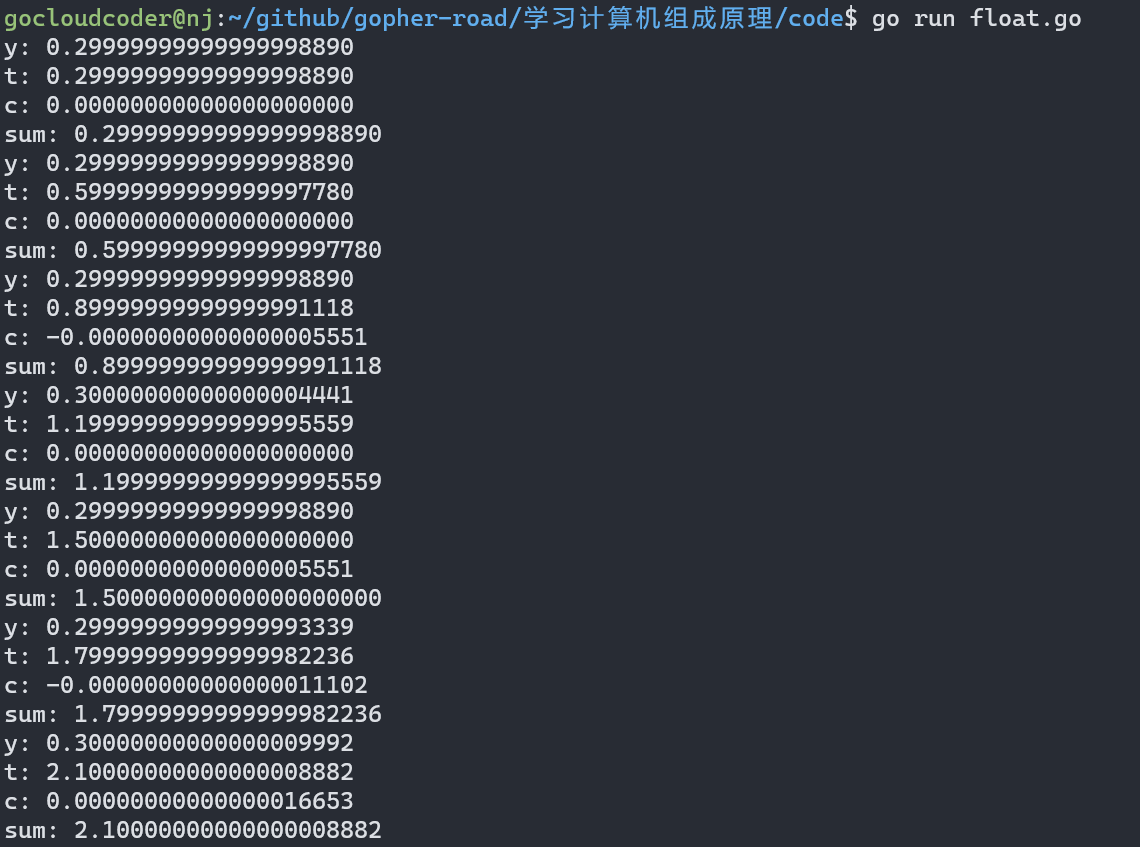
通过这么几行代码我们就实现了避免精度损失。所以算法还是蛮重要的哦！